RaBitQ: Quantising High-Dimensional Vectors with a Theoretical Error Bound for Approximate Nearest Neighbor Search

Opportunity

Nearest neighbour search is essential for applications in information retrieval, vector databases and machine-learning systems. Currently, product quantisation (PQ) is the mostly widely used method for speeding up nearest neighbor search but lacks a theoretical guarantee, leading to unpredictable accuracy. RaBitQ addresses this by providing a method that efficiently and unbiasedly estimates the distances between two high-dimensional vectors with a proven asymptotically optimal error bound. This ensures robust performance, making RaBitQ a potential replacement for PQ in database and machine-learning systems.

Technology

RaBitQ constructs a quantisation codebook using randomly rotated bi-valued unit vectors. For each data vector in a database, it finds the nearest vector in the codebook for quantisation. The method then constructs an unbiased distance estimator by analysing the geometric relationship among the query, data and quantised vectors, unlike PQ which estimates distances by treating the quantised vector as the data vector. RaBitQ introduces two implementation versions for efficient distance estimation: one using bitwise operations for single data vectors and another using single instruction/multiple data (SIMD)-based operations for batched data vectors.

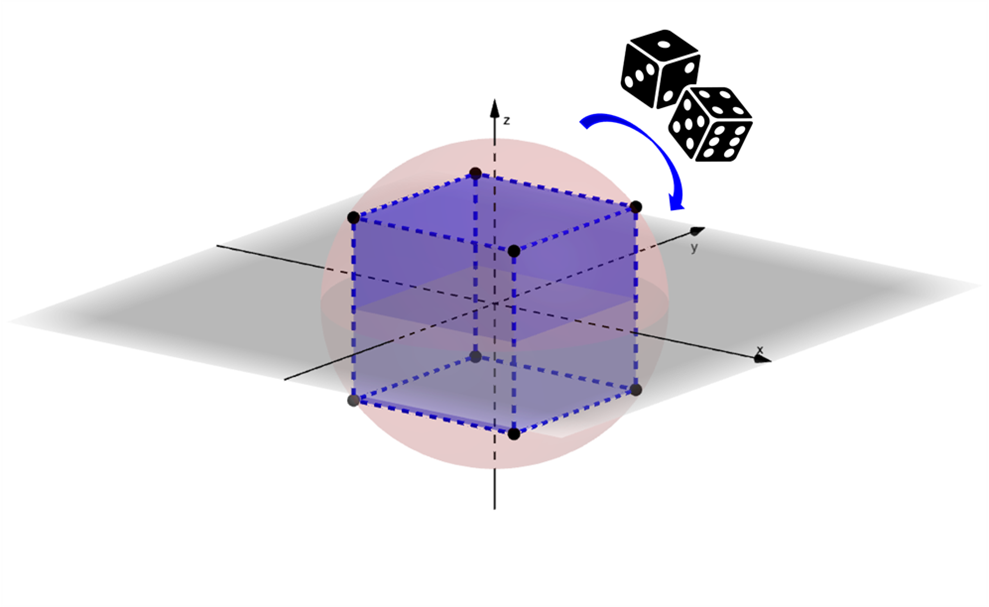
Figure 1: The codebook of RaBitQ is a randomly rotated hypercube.

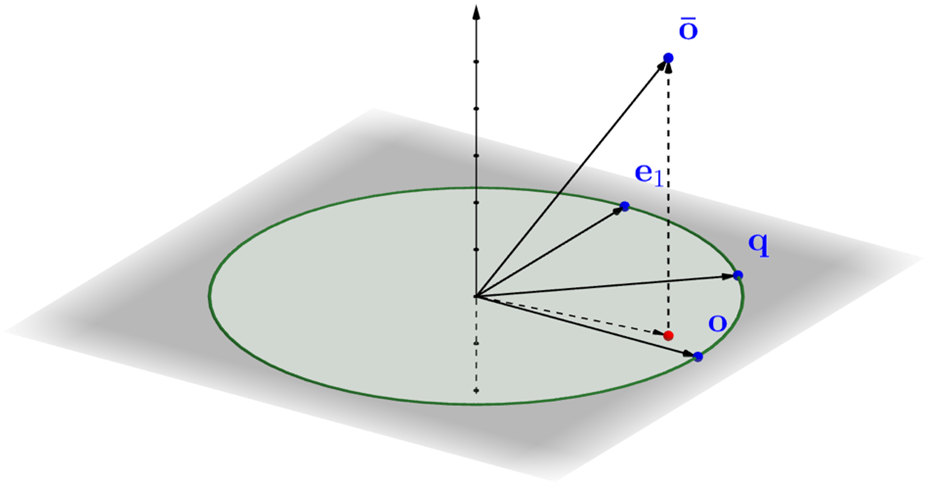
Figure 2: The distance estimator of RaBitQ is constructed by explicitly analysing the geometric relationship among the query, data and quantised data vectors.

Applications & Advantages

Main application areas include vector database systems, machine-learning systems, search engines, e-commerce systems and recommendation systems.

Advantages:

• Provides a theoretical error bound guaranteeing robust performance
• Ensures accurate distance estimation compared to PQ
• Utilises bitwise and SIMD-based operations for speed and efficiency
• Demonstrates significant improvements on real-world datasets, including scenarios where PQ fails